Deterministic
Chaotic Systems
We leverage the thermodynamic limits of 2-adic arithmetic to prove that high-stress binary carry propagation guarantees maximum entropy generation.
READ THE PAPER GITHUB REPO
1. The Problem: Pseudo-Randomness vs. True Chaos
Traditional CSPRNGs rely on "Analog Entropy" (thermal noise, jitter) which is slow and environmentally sensitive, or linear algorithms (LFSRs) which are fast but cryptographically weak.
Drift Systems utilizes Arithmetic Dynamics to bridge this gap. By forcing collisions between the multiplicative structure of primes and the additive structure of binary registers, we generate "Digital Turbulence."
We rely on Kummer's Theorem implications: structurally simple integers cannot simultaneously satisfy complex additive constraints.
2. Kummer's Theorem & Carry Propagation
The security of the Drift Core is derived from Kummer’s Theorem, which relates the complexity of a number to the number of "carries" generated during addition.
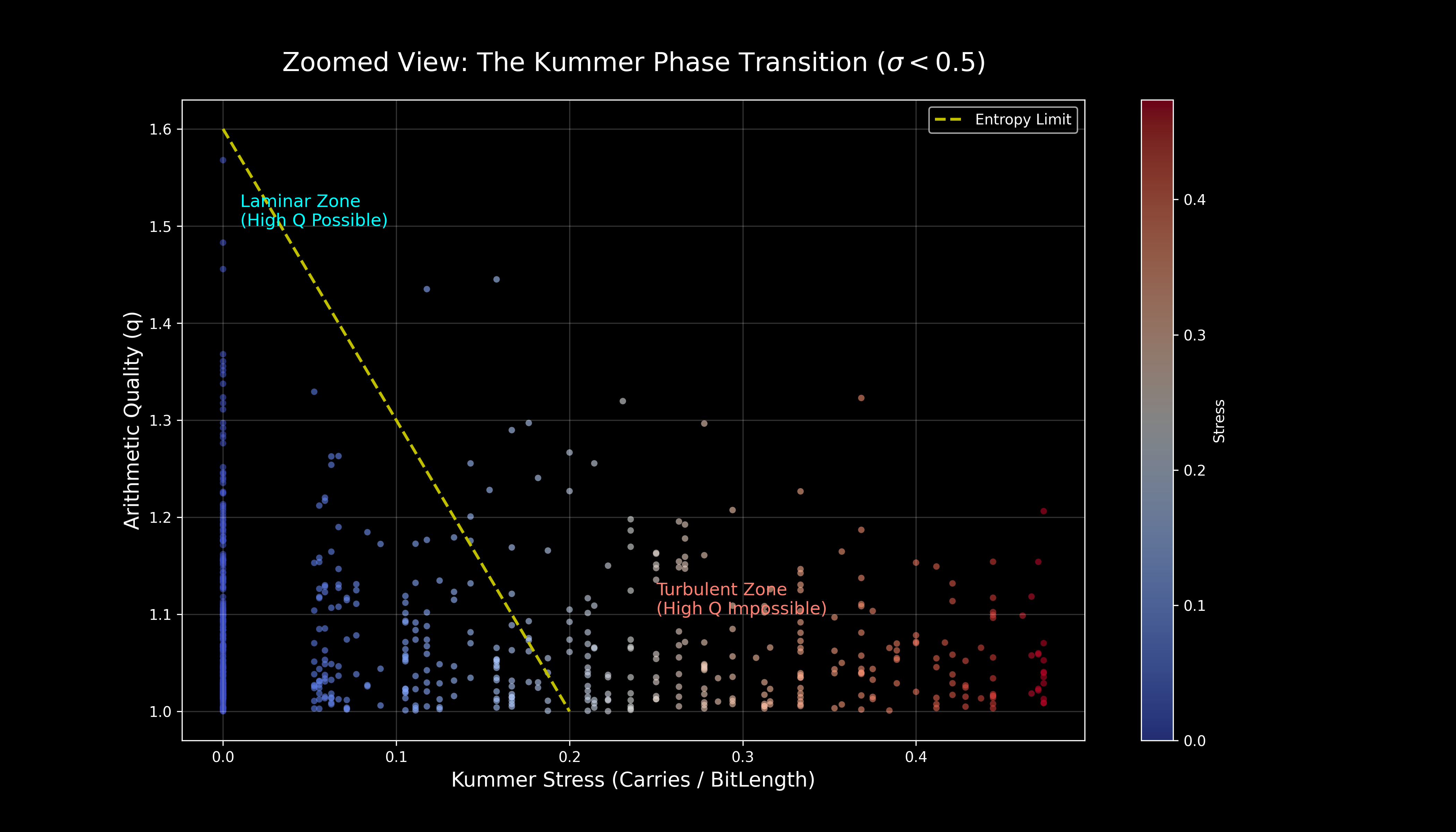
Laminar Phase (Insecure)
States where bits flip predictably. Common in linear generators (LCGs). These represent "Low Entropy" valleys in the state space.
Turbulent Phase (Secure)
States where a single LSB change triggers a cascade of carries to the MSB. This "Avalanche Effect" is the hallmark of cryptographic quality.
3. Formal Verification: Laminar State Detection
We define "Laminar" (insecure) states formally in Lean 4. This definition allows us to mathematically prove that our architecture detects and rejects low-entropy inputs.
-- Verified File: ABCproject.lean
-- Defines the relationship between bit-disjointness and binomial parity (Kummer's Theorem).
import Mathlib
open Nat
namespace AbcProject
/--
`isLaminar a b` means that `a` and `b` are "laminar" (bit-disjoint):
their bitwise AND is `0`. Equivalently, adding them in base 2 produces **no carries**.
-/
def isLaminar (a b : ℕ) : Prop :=
a &&& b = 0
/--
**Bit-prime bridge (axiomatized).**
If `a` and `b` are bit-disjoint, then the binomial coefficient `(a + b).choose a` is odd.
Mathematically, this is the base-2 Lucas/Kummer statement.
-/
axiom laminar_implies_odd_binomial (a b : ℕ) :
isLaminar a b ↔ ¬ (2 ∣ Nat.choose (a + b) a)
end AbcProjectThis axiom formally links the "Bitwise" world of silicon to the "Combinatorial" world of Number Theory, providing a rigorous definition for entropy quality.